NumberPad - Discovering Laws of Math
- 6 minsDiscovering Laws of Math
One amazing part of mathematics is that the laws are universal. You don’t need to be told that for every circle \(\frac{circumference}{diameter} = 3.14159....\), because you can discover it yourself. If we met aliens, we’d expect they’d have discovered these same truths. Kinda crazy!
Doing real math is discovering and proving new relationships. Doing math in a classroom is not like this at all. Could we set up students to discover these laws for themselves?
I’ve created a few puzzles in NumberPad for discovering these universal truths independently. I’m inspired by video games which put you on the right path and give just enough clues, but still have you feeling 💃😁🎉 when you solve it.
(If you haven’t read about NumberPad yet, check out this previous post to see the basics. This post will be a lot more interesting with that context.)
For this puzzle, pretend you don’t know that you haven’t learned about \(\pi\) yet. Let’s discover it.
We’ve got a circle. You can change the diameter:
You can play with the circumference, and try to make it match up with the circle. When it does match up, it turns dark blue.
The point of this puzzle is to figure out the relationship between those two numbers so that it will work for every circle. NumberPad only supports addition, multiplication, and exponentiation, so let’s just pick one and try it. Maybe the relationship is \({diameter}^{something?} = {circumference}\)
For this circle, that “something” was \(1.50\). Does that work for other circles? Have we discovered a law of the mathematical universe? We can change the diameter and see the circumference change.
Hmm, nope. The circumference changed with the diameter but the new circumference didn’t line up. There is an easier way to see how wrong our guess it. We can show other circles with different diameters and see that our guess overshoots the circumference on the big circles and undershoots the diameter on small circles.
Making mistakes is okay. Let’s try anotehr simple relationship. Maybe (just maybe), it is \({diameter} * {something?} = {circumference}\).
For those of you in the know, the \(3.14\) is pretty promising. Let’s try it on other circle sizes.
What do you know?! It works on those other circles too! Maybe this relationship is universal? How weird that it depends on such a specific number like \(3.14\)… I wonder if that number ever comes up in other places? 😉
What is more fun than a circle? How about a square!?! 😮 This next puzzle is leading up to a pretty great one, so it is worth it.
With this square we can control the side length:
And we want to figure out the area of the square. For this one, we can tell it is \(81\) because everything lines up and turns a nice color.
We’ve got to find a relationship that ties those numbers together, but works for all squares. An enterprising (but, as we know, wrong) student might think the relationship is \(length * something = area\). Let’s see how that plays out.
Hrmmm. The area starts out too big on the small squares and doesn’t grow fast enough for the big squares. Let’s try a relationship that grows faster. EXPONENTIATION!
Sweet! It works for all the squares we care to test. We’ve discovered another law of the universe! 🏆
That set’s us up for the best puzzle I’ve programmed so far……
THE PYTHAGOREAM THEOREM!!!!! 😲
In this puzzle we can change the length of the blue line or the green line, and we are trying to figure out how big the orange line should be. We want that orange square to be all dark colored.
This puzzle could probably use some stars and sparkles when you get the right answer. 🤔 Open source contribution, anyone?
For this puzzle, randomly guessing relationships won’t be very successful. First, let’s do a part that we know. Those blue, green, and orange squares?
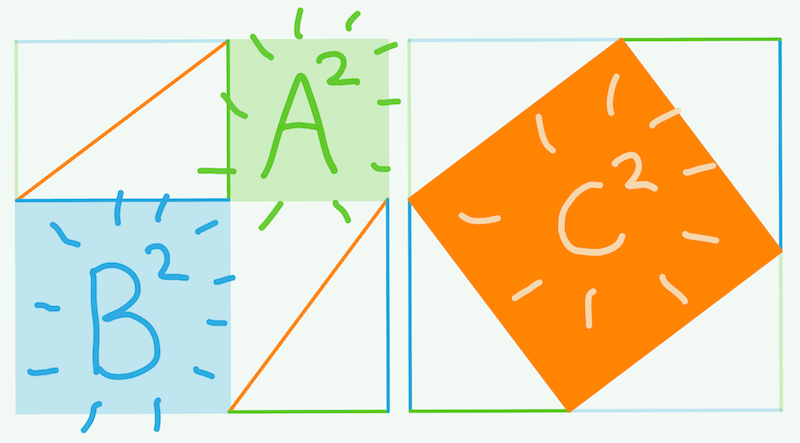
From the last puzzle we know how to make a square’s area. Let’s do that for each one.
Maybe this is progress, but what is the relationship between those squared numbers? For this part we’ll need a clever breakthrough, which we can get by studying the shapes.
There are two large squares of the same size. Each of those large squares has 4 triangles in it. Each triangle is the same size because they each have a blue, green, and orange side.
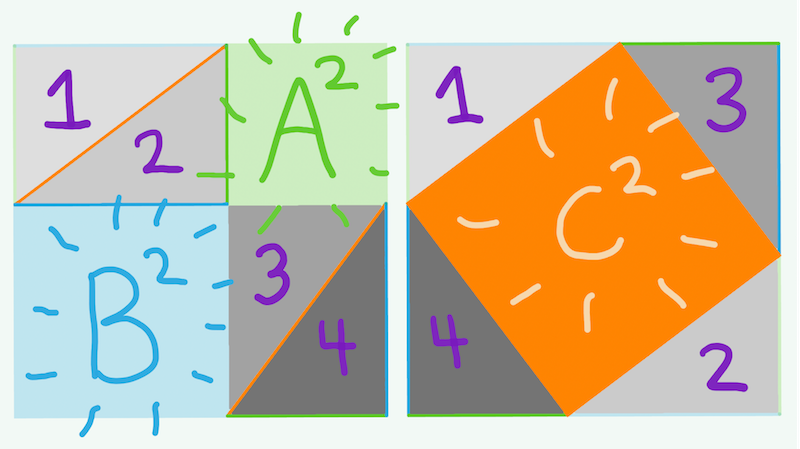
So, if we take away the four triangles, what is left? On one side we have the blue and green squares. One the other side we have the orange square.
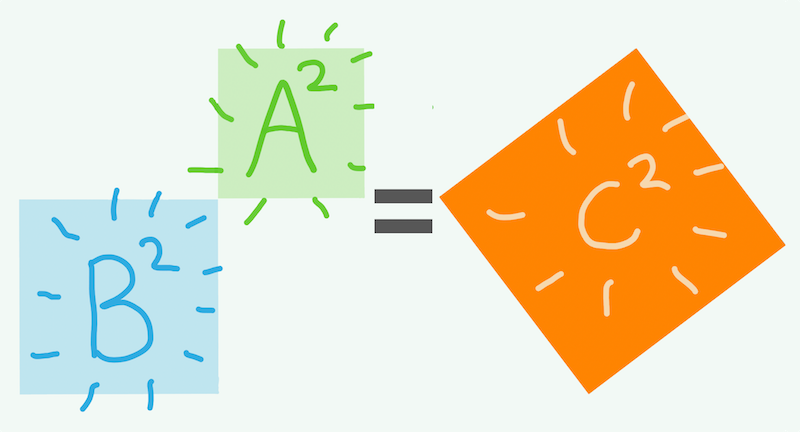
The blue and green square must be the same size as the orange! We try adding them together…..
And voila! We’ve figured out the relationship between green, blue, and orange (or \(a\), \(b\), and \(c\), if you prefer). We can change the green number and our newfound relationship, \(a^2 + b^2 = c^2\) finds the new orange number.
We can even change the orange number and solve for the new blue number.
These puzzles show just the beginning of what could be done in Numberpad. Imagine trying to do these same puzzles with pencil and paper worksheets. In the words of Donald Trump, it would be a disaster.
The machanics of algebra on paper make it difficult to discover something new. It is more likely that a student would make an error like \({(a + b = c)}^2\). Worse, that student wouldn’t even know that was a mistake until the worksheet came back graded a few days later.
In Numberpad, a student has the freedom to play with math knowing they won’t accidentally “break the rules”.
If you think NumberPad could be used in a classroom, please reach out. I’d love to turn these prototypes into a curriculum. Email me at bridger.maxwell@gmail.com or find me on Twitter as @bridgermax.
